Superenalotto
Le vere probabilità
di vincita del gioco a premi più popolare d'Italia
 Fra
il 3 febbraio 2009 (concorso N° 15) ed il 20 agosto del 2009 (concorso N°100),
nessuno riuscì a centrare il mitico 6 al Superenalotto, facendo
quindi levitare il montepremi del Jackpot fino alla stratosferica cifra di 147.807.299,08
€, poi vinti il 22 agosto con un biglietto giocato alla ricevitoria di un bar di Bagnone (Massa
Carrara).
Fra
il 3 febbraio 2009 (concorso N° 15) ed il 20 agosto del 2009 (concorso N°100),
nessuno riuscì a centrare il mitico 6 al Superenalotto, facendo
quindi levitare il montepremi del Jackpot fino alla stratosferica cifra di 147.807.299,08
€, poi vinti il 22 agosto con un biglietto giocato alla ricevitoria di un bar di Bagnone (Massa
Carrara).
La cosa più
strabiliante però, dal punto di vista statistico, e non osservata da nessuno, non è tanto il numero di concorsi
senza vincitori, bensì il fatto che nel precedente concorso vincente (il N°
14), ben 5 concorrenti avevano realizzato il 6! A parte l'anomalia
statistica, si trattò in quel caso
di persone fortunatissimamente sfortunate, in quanto dovettero dividere
il montepremi fra loro, incassando appena 7.947.183,69 € a testa...
Ancor più fortunatamente
sfortunata fu la persona che azzeccò il 6 nell'estrazione del 22 maggio
2007: poiché appena due giorni prima, nel concorso precedente, era stato
realizzato un altro 6 da 71.439.610,83 €, il Jackpot non aveva avuto modo di
crescere, ed il poveretto dovette
accontentarsi di soltanto 1.709.467,29 €...
Un po' come in una
vecchia storia apparsa su Topolino negli anni '70, credo (forse era "Gastone
e la fortuna sfortunata", o qualcosa di simile... 
 comunque
NON questa
storia, che è ben più tarda, del '91), in cui Paperino e Gastone cozzano
casualmente con la testa fra loro, e come conseguenza ciascuno dei due assorbe
un po' delle peculiarità dell'altro. Per cui a Gastone finisce ancora per andar
sempre bene, ma a costo di inenarrabili vicissitudini che gli fanno sospettare
di aver perso la sua proverbiale buona sorte, mentre Paperino si avvicina più
volte ad un nonnulla da indicibili fortune, che poi come sempre alla fine
svaniscono... Ecco, i 6 protagonisti delle vincite di cui sopra sono un po' come
il Gastone di quella storia, e ne vengono quindi fuori più che bene, ci
mancherebbe, ma con il rammarico immenso dell'aver perso per un pelo il
colpaccio strepitoso... In un ipotetico Club dei vincitori del Superenalotto,
costoro sarebbero degli emarginati, dei vincitori di second'ordine... Senz'altro
demerito dell'essere capitati come vincenti in casi di anomalia statistica...
comunque
NON questa
storia, che è ben più tarda, del '91), in cui Paperino e Gastone cozzano
casualmente con la testa fra loro, e come conseguenza ciascuno dei due assorbe
un po' delle peculiarità dell'altro. Per cui a Gastone finisce ancora per andar
sempre bene, ma a costo di inenarrabili vicissitudini che gli fanno sospettare
di aver perso la sua proverbiale buona sorte, mentre Paperino si avvicina più
volte ad un nonnulla da indicibili fortune, che poi come sempre alla fine
svaniscono... Ecco, i 6 protagonisti delle vincite di cui sopra sono un po' come
il Gastone di quella storia, e ne vengono quindi fuori più che bene, ci
mancherebbe, ma con il rammarico immenso dell'aver perso per un pelo il
colpaccio strepitoso... In un ipotetico Club dei vincitori del Superenalotto,
costoro sarebbero degli emarginati, dei vincitori di second'ordine... Senz'altro
demerito dell'essere capitati come vincenti in casi di anomalia statistica...
A parte gli
esempi di cui sopra ai limiti dell'aneddotica (non è questo il tema di questa pagina),
l'escalation dell'interesse generale dell'estate 2009 sul montepremi del
Superenalotto mi aveva spinto a cercar di calcolare
le varie probabilità di fare 6, 5+1 eccetera, per puro sollazzo statistico/matematico... Il calcolo della probabilità di far 6 è abbastanza
semplice, per il 5+1 ed il 5 le cose sono più complesse; ho cercato un po' in
giro con GoogleTM,
e sono alla fine rimasto abbastanza stupito nello scoprire che i pochi siti che
riportano i valori delle probabilità (anche quelli completi dei calcoli)
presentano valori sempre o quasi sbagliati (e, spesso, clamorosamente
diversi fra loro)! Nessuno dei siti da me esplorati riporta tutti i
valori corretti, c'è sempre un errore per almeno uno di essi!
Chi legge potrebbe
chiedersi come possa io vantar d'esser certo che calcoli e valori che seguono
siano invece esatti; ovviamente infatti non posso esserne sicuro al 100%, e se
qualcuno trovasse qualche pecca nel seguito sarei ben contento di accettare suggerimenti e
correzioni. Resta il fatto che ho eseguito tutte le possibili verifiche che mi
sono venute in mente, trovando conferma per i risultati, così come di seguito
esposto.
La maggior parte degli
errori rilevati nei vari altri siti riguarda le valutazioni per il caso del 5: quasi
sempre viene inglobata la probabilità di far 6 in quella di far 5. E' ovvio che
un 6 contiene in sé anche sei 5, ma le regole
prevedono che venga pagato il solo 6, se vincente, non anche i 5 collaterali. Inoltre,
praticamente nessuno scorpora il caso del 5+1 da quello del 5, ed il tutto porta alla
sopravvalutazione della probabilità di fare un 5 secco...
Nel seguito si sottintende
sempre, salvo diverso avviso, che i calcoli riportati siano relativi alla giocata
di una sola sestina; per più sestine, se non sono troppe, la
probabilità complessiva di vincita si ottiene quasi moltiplicando il
numero di differenti sestine giocate per le varie probabilità. In realtà ciò
non è matematicamente corretto, poiché non tiene in conto le probabilità
condizionali (la probabilità di fare 3 è circa 1/327; non è però vero che
giocando 327 sestine si abbia la certezza di fare 3...). E' poi noto che per regolamento
occorre giocare almeno 2 sestine; ciononostante, i calcoli che seguono si
riferiscono ad una sestina singola.
Infine, non si è
considerato in questo contesto il numero Superstar; in effetti, non so neppure
bene come
funzioni, dal momento che non me ne sono mai interessato...
Qui di seguito l'indice
dei temi trattati in questa pagina:
Il
numero di diverse possibilità
In quanti modi diversi
può presentarsi il risultato di una qualsiasi estrazione del Superenalotto, e
come si ripartiscono le vincite? Il
calcolo non è così banale come per il Totocalcio, dove (all'epica epoca del 13) le
diverse possibilità erano 313,
e nemmeno di media complessità come per il Lotto, sebbene quest'ultimo si
avvicini di più al Superenalotto. Le complicazioni derivano dalla presenza del
numero Jolly, che serve per determinare le vincite per il 5+1, in particolare poiché
le regole di estrazione sono tali che il Jolly viene gestito in modo diverso dai
numeri della sestina base.
Quando viene estratto
il primo numero (non coi mezzi dell'immagine sotto a sinistra; oggi si utilizza un
complicato marchingegno pneumatico a prova di imbrogli, almeno si spera...), vi
sono 90 valori diversi che questo può assumere; per il secondo 89 valori relativi ai
rimanenti numeri, e così via fino ad 85 per il sesto numero. Il numero di modi in cui
i 6
numeri possono venire estratti è quindi:

Ma, per le regole del
gioco, la sequenza di estrazione non ha alcuna importanza; due estrazioni che
producessero le sestine:
 (45,
31, 78, 2, 29, 16) e (29, 16, 31, 78, 45, 2)
(45,
31, 78, 2, 29, 16) e (29, 16, 31, 78, 45, 2)
sarebbero del tutto
equivalenti per l'attribuzione dei premi, e verrebbero presentate entrambe nello
stesso usuale ordine crescente:
(2, 16, 29, 31, 45, 78)
Poiché 6 numeri
distinti possono comparire in:

ordinamenti diversi,
nei 448 miliardi e rotti di possibilità ciascuna sestina riordinata appare 720
volte; il numero effettivo di sestine da considerare è quindi dato da:

Tutto ciò
relativamente alla sestina base; dopo di essa viene estratto il numero Jolly fra
i rimanenti. Contrariamente ai primi 6 numeri, quest'ultimo non viene
riordinato: a ciascuna delle sestine può abbinarsi allora uno qualsiasi
degli 84 numeri residui, per cui la quantità globale di possibilità per il
complesso dei 7 numeri estratti è:

In pratica però, il
Jolly ha significato esclusivamente per le sestine giocate che realizzano un 5;
su di esse l'effetto del Jolly può essere il trasformarle in un 5+1 o, più
probabilmente, nel lasciarle vincenti come 5. Le sestine che per ogni data
estrazione realizzano 6, 4, 3, 2, 1 o 0 punti non sono influenzate in alcuna
maniera dal valore del numero Jolly; per il 6, un 6+1 non è nemmeno
concepibile, per gli altri valori le sestine che realizzano, poniamo, un 3+1 o
un 2+1 rimangono rispettivamente vincenti o perdenti nelle relative categorie
dei 3 e dei 2.
Nel seguito, si inizia
col calcolare le ripartizioni di possibilità di vincita (o non vincita) fra le
varie categorie, ipotizzando inizialmente che il 5+1 non esista, o meglio
che sia conglobato nel 5. Questo fornisce i valori corretti per tutte le
categorie tranne la 5 e la 5+1, che vengono poi trattate separatamente.
Cosa
farsene di tutte queste possibilità
Per quanto sopra, se
un'oretta dopo una qualsiasi estrazione andiamo frementi a consultare la pagina
598 del Televideo,
la lista di 7 numeri che apparirà sarà una fra le 52·299·628·920
possibili; come anticipato sopra, occupiamoci al momento della sola sestina
base, senza considerare il numero Jolly. Le possibili combinazioni da prendere in
considerazione ammontano allora a 622·614·630, come
visto in precedenza.
 Un certo numero di esse
permette di far 6, un altra
quantità 5, e così via. In sostanza, per ciascuna sestina da noi giocata,
l'esito può essere uno ed uno solo fra i seguenti 7 casi:
Un certo numero di esse
permette di far 6, un altra
quantità 5, e così via. In sostanza, per ciascuna sestina da noi giocata,
l'esito può essere uno ed uno solo fra i seguenti 7 casi:
-
La
sestina ottiene un 6; ciò capita per N6
dei 622·614·630
casi
-
La sestina
ottiene un 5; ciò capita per N5
dei 622·614·630 casi
-
La sestina
ottiene un 4; ciò capita per N4
dei 622·614·630 casi
-
La sestina
ottiene un 3; ciò capita per N3
dei 622·614·630 casi
-
La sestina
ottiene un 2; ciò capita per N2
dei 622·614·630 casi
-
La sestina
ottiene un 1; ciò capita per N1
dei 622·614·630 casi
-
La sestina
ottiene uno 0; ciò capita per N0
dei 622·614·630 casi
Poiché una singola
sestina non può contemporaneamente realizzare, poniamo, sia un 2 che un 3, e poiché in uno
dei 7 casi di cui sopra essa deve pur ricadere, deve essere necessariamente:
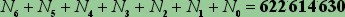
I termini N6,
N5, ...,
N0
rappresentano il numero di possibilità di realizzare rispettivamente 6,
5, ..., 0. Per ottenere le relative probabilità di realizzazione dei
vari punteggi, basta dividere ciascun numero di possibilità per i casi
possibili complessivi, cioè per 622·614·630.
Se denominiamo P6,
P5, ...,
P0
tali probabilità, dovrà allora essere:
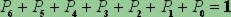
Spesso il concetto di
probabilità viene espresso non come numero decimale (minore di 1) quali sono le
varie P definite sopra, bensì in termini dialettici tipo una possibilità su 100·000,
e ciò per dare l'idea di quante volte si dovrebbe giocare per avere una singola
concreta opportunità di vincita; si trasformano cioè i valori P di cui sopra in frazioni con
numeratore unitario. Se utilizziamo la lettera M per definire i denominatori di
tali frazioni, la precedente relazione diventa:
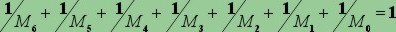
Mi rendo conto di esser
stato un po' pedante in questa esposizione, e che molti abbiano ormai
abbandonato la lettura per attività ben più gratificanti; ritengo però che molti
degli errori riscontrabili in giro nei vari siti che trattano l'argomento
derivino proprio dal non aver considerato le regole basilari esposte sopra.
Primo fra tutti, l'errore di attribuire i casi riferibili al 6 anche al 5
(contravvenendo alla regola che l'esito per ciascun caso possibile può essere uno
ed uno solo fra i 7 citati), o tralasciando di valutare i casi di non
vincita (2, 1 e 0), utilissimi invece per verificare che le somme di cui sopra siano
consistenti.
Nei prossimi paragrafi
si calcoleranno i valori dei vari fattori N, da cui è poi facile risalire ai
valori dei fattori P ed M.
 La probabilità
di far 6
La probabilità
di far 6
Il calcolo di N6
è il più semplice di tutti; c'è una ed una sola sestina base ordinata che
garantisca la vincita, quella per cui tutti i 6 numeri estratti (Jolly escluso) coincidono con i
6 giocati. Quindi N6
è pari ad 1, per cui:

Il calcolo di M6
appare un po' lezioso, sapevamo già di avere una sola possibilità
su 622·614·630;
ciò capita perché N6
è proprio pari ad 1. Si vedrà che negli altri casi, il valore di M è più
significativo, quando N assume valori diversi.
 La probabilità
(provvisoria) di far 5
La probabilità
(provvisoria) di far 5
Vediamo come valutare N5;
consideriamo la combinazione vincente, quella che realizza il 6. La sestina
giocata, per realizzare 5, deve avere in sé uno qualsiasi (ed uno solo) dei 6 numeri sbagliato:
cioè al posto di uno dei 6 numeri vincenti deve essercene uno (solo uno, ma uno,
non nessuno!) degli 84 non
estratti. Quindi tutte le sestine che realizzano 5 si ottengono alterando in 84
modi diversi ciascuno dei 6 estratti, cioè:

Quindi fare 5 è 504
volte più probabile che far 6, ma attenzione! Questa probabilità contiene in sé
anche quella di realizzare un 5+1! Per il momento accontentiamoci, restando dubbiosi, e manteniamo
i valori trovati come provvisori...
La probabilità
di far 4
Con N4
le cose si complicano un po'... Ripartiamo dalla sestina vincente: per
trasformarla in una che realizza un 4 bisogna alterare 2 dei numeri vincenti in
altrettanti numeri sbagliati, in tutti i modi possibili. Supponiamo che
la combinazione vincente sia la (2, 16, 29, 31, 45, 78) presa ad  esempio
in precedenza; i due numeri da alterare possiamo sceglierli in 15 modi diversi,
indicati in rosso
nella tabella che segue:
esempio
in precedenza; i due numeri da alterare possiamo sceglierli in 15 modi diversi,
indicati in rosso
nella tabella che segue:
| (2,
16,
29, 31, 45, 78) |
(2,
16, 29,
31, 45, 78) |
(2,
16, 29, 31,
45, 78) |
(2,
16, 29, 31, 45,
78) |
(2,
16, 29, 31, 45, 78) |
| (2, 16,
29,
31, 45, 78) |
(2, 16,
29, 31,
45, 78) |
(2, 16,
29, 31, 45,
78) |
(2, 16,
29, 31, 45, 78) |
(2,
16, 29,
31,
45, 78) |
| (2,
16, 29,
31, 45,
78) |
(2,
16, 29,
31, 45, 78) |
(2,
16, 29, 31,
45,
78) |
(2,
16, 29, 31,
45, 78) |
(2,
16, 29, 31, 45,
78) |
Le scelte possibili
sono 15 poiché il primo dei due numeri possiamo sceglierlo in 6 modi diversi,
ed il secondo fra i 5 rimanenti, quindi 6·5=30 possibilità; ma l'ordine con
cui vengono selezionati i due numeri da alterare non ha importanza (2 e
16 oppure
16 e
2 ha lo
stesso effetto), per cui i casi da considerare sono la metà. Questa
osservazione tornerà utile per le probabilità successive, quando verrà estesa
a quei casi.
Per ciascuno dei 15
modi elencati, dobbiamo poi considerare 2 fra gli 84 numeri sbagliati
potenzialmente possibili e
posizionarli al posto dei numeri rossi:
il primo di essi possiamo sceglierlo ovviamente in 84 modi diversi, il secondo
fra i rimanenti 83, quindi nel complesso 84·83=6·972
possibilità. Ma, ancora una volta, attenzione! Data una qualsiasi coppia di
numeri sbagliati scelta (poniamo siano 11 e 63), essa appare due volte
nelle suddette 6·972 possibilità (l'11 per primo ed il 63 per secondo, o
viceversa), e non fa differenza se
sostituiamo l'11 al 2 ed il 63 al 16, oppure il contrario, poiché ai fini del
regolamento non conta l'ordine in cui i numeri appaiono nella sestina
finale; dobbiamo quindi ancora
dimezzare il numero di combinazioni che vengono fuori. In definitiva si può
scrivere:

La probabilità
di far 3
Con N3
sarebbe ancora più contorto... Ma se estendiamo quanto visto per N4,
le cose non dovrebbero essere troppo difficili... Ricominciando sempre dalla
sestina vincente, per trasformarla in una che realizza un 3 bisogna alterare 3
numeri, rendendoli sbagliati. I numeri da alterare possono essere scelti in 6·5·4=120
modi diversi, ma ancora una volta bisogna ignorare l'ordine con cui sono scelti,
per cui questo fattore va diviso per 3·2=6 (6 sono infatti i modi in cui possono essere
riordinati 3 diversi numeri, ad esempio così: ABC, ACB, BAC, BCA, CAB, CBA). I 3
numeri sbagliati che vanno a sostituire quelli buoni da
togliere potranno adesso essere scelti in 84·83·82 modi diversi, ed ancora dividiamo
questo fattore per 3·2, in quanto come sempre non interessa l'ordine di
estrazione, stavolta dei numeri sostituti. Quindi:

La probabilità
di far 2
Perché mai ci
interessiamo della probabilità di far 2? In fondo, non è vincente,
anzi: è quella che maggiormente fa incaz... Beh, semmai qualcuno è
interessato a sapere con che cadenza può aspettarsi di potersi incavolare,
però ciò serve maggiormente per altre ragioni.
Primo, per completezza
espositiva: le varie probabilità di occorrenza vanno valutate prescindendo dal
fatto che siano vincenti o no, è una questione di uniformità matematica; poi
potrebbero cambiare i regolamenti, e semmai anche il 2 diventerebbe vincente...
Ancora, il calcolo dei casi in cui si fa 2 serve, come si vedrà, per la
verifica dei risultati...
Comunque, per N2,
si dà per scontato che il metodo
visto per N3
sia chiaro... Quanto visto per N3
si estende facilmente come segue:

 La probabilità
di fare 1
La probabilità
di fare 1
Per
N1,
si ha poi, sempre continuando come sopra:
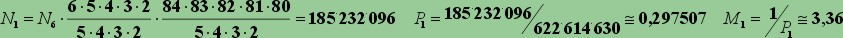
La probabilità
di far 0
Infine, per N0,
si giunge stremati a quanto segue:

Qualche
verifica intermedia...
Prima di procedere col
caso del 5+1, facciamo qualche controllino che i risultati ottenuti siano
coerenti. Sempre assumendo che il 5+1 non esista, la somma delle varie possibilità di occorrenza dei singoli risultati
deve corrispondere al totale delle combinazioni possibili; infatti si ha:


Un'altra verifica può
essere eseguita ragionando su N0;
nel paragrafo precedente esso è stato ricavato estendendo le formule utilizzate
precedentemente per N4,
N3,
eccetera, fino ad N0
appunto. Se si rammenta come sono state costruite, per queste si partiva da N6,
calcolando in quanti modi questo potesse essere modificato per ottenere via via
sestine in grado di produrre un 4, un 3, e così via fino a nessuna, cioè N0.
Ma N0
può anche essere calcolato diversamente, dal punto di vista concettuale. Vediamo come: il
numero di modi in cui il primo estratto può non appartenere alla sestina
giocata è 84 (dei 90 numeri, tutti tranne i 6 estratti); il secondo estratto, per essere anch'esso fra i non appartenenti
alla nostra sestina, può essere
scelto in 83 modi diversi, e così via. Affinché tutti i 6 estratti non facciano parte
della sestina giocata (quindi, per realizzare 0, sai che soddisfazione...), vi sono allora 84·83·82·81·80·79
possibilità. Ancora una volta, l'ordine di estrazione non ha alcuna influenza,
per cui occorre dividere per il fattore che dà conto del numero di modi
possibili di apparizione dei 6 numeri, come segue:

Naturalmente, questa
relazione fornisce lo stesso risultato ricavato in precedenza; ma essendo stato
completamente ribaltato il processo logico di costruzione della formula, essa
costituisce una forte conferma della validità dei calcoli eseguiti.
La probabilità
di far 5+1
E adesso si può andare
a vedere cosa succede quando si prende in considerazione il numero Jolly...
Secondo il regolamento
del gioco, soltanto le sestine giocate che hanno realizzato un 5 sono
interessate al valore del numero Jolly; le altre, vincenti con 6, 4 e 3 punti,
oppure perdenti con 2, 1 o 0 punti, non saranno influenzate in alcun modo.
Quindi i valori di N6,
N4,
N3,
N2,
N1
ed N0,
nonché i valori di P ed M ad essi associati, non cambieranno per nulla.
Solo N5
(con P5
ed M5
di conseguenza), subirà modifiche; vediamo come. Si ricorda che N5=504;
ciò vuol dire che esistono 504 possibili sestine giocate che hanno 5 numeri corretti ed
uno sbagliato; per realizzare il 5+1 con una qualsiasi di esse occorre
che il numero Jolly coincida proprio con il numero sbagliato
contenuto in ciascuna di esse.
Il numero Jolly viene
estratto dopo i 6 numeri vincenti, indipendentemente da essi, fra gli 84
numeri residui: vi è allora una sola possibilità su 84 che esso coincida proprio con
il numero sbagliato, per ciascuna delle 504 sestine che realizzano il 5.
Quindi:
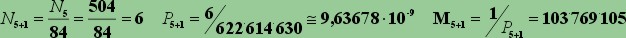
Ed è quindi 6 volte
più probabile realizzare un 5+1 anziché un 6...
La probabilità
(definitiva) di far 5
Poiché fra i 504
generici modi
di realizzare un 5, 6 di essi cambiano di categoria secondo regolamento
(salendo
in quella del 5+1) il reale numero di possibilità in grado di realizzare un 5
secco scende corrispondentemente di tale quantità... Si ha allora:

Riepilogo
E finalmente, il
traguardo è raggiunto, e si possono riepilogare i risultati conseguiti, qui
nella tabella che segue:
| Probabilità
di realizzare i vari punteggi al gioco del Superenalotto |
| Punteggio |
Possibilità |
Probabilità |
1 /
Probabilità |
Rapporto
N / (N+1) |

|
| 6 |
1 |
~1,60613·10-09 |
622·614·630 |
N.A. |
| 5+1 |
6 |
~9,63678·10-09 |
103·769·105 |
6 |
| 5 |
498 |
~7,99853·10-07 |
~1·250·230 |
83 |
| 4 |
52·290 |
~8,39845·10-05 |
~11·907 |
105 |
| 3 |
1·905·680 |
~3,06077·10-03 |
~327 |
36,4 |
| 2 |
28·942·515 |
~4,64854·10-02 |
~21,5 |
15,1875 |
| 1 |
185·232·096 |
~0,297507 |
~3,36 |
6,4 |
| 0 |
406·481·544 |
~0,652862 |
~1,53 |
2,194 |
| Totali |
622·614·630 |
1 |
N.A. |
N.A. |
Qualche chiarimento sulla tabella, per
chi arrivasse qui senza essere interessato a leggere tutto quanto esposto sopra
o sotto,
e comunque a titolo di compendio:
- La prima colonna mostra
tutti i
possibili punteggi conseguibili giocando una singola sestina al
Superenalotto
- Essendovi 622·614·630
possibili diverse sestine base estraibili in ciascun concorso, la seconda
colonna mostra quante di esse permettono di conseguire il punteggio
riportato nella prima colonna; ad esempio, esistono 52·290
sestine che permettono di ottenere un 4
- La terza colonna contiene
semplicemente il rapporto, per ogni riga, fra il valore riportato nella
seconda colonna ed il numero complessivo di possibilità, cioè 622·614·630

- La quarta colonna contiene i valori reciproci di quella precedente; essa indica ogni
quante giocate (di singole sestine) ci si può aspettare di conseguire il
punteggio della prima colonna. Ad esempio, giocando una sestina ad ogni
estrazione, si può sperare di ottenere 3 più o meno ogni 327 estrazioni, cioè una vincita (col 3) ogni 2 anni, assumendo come adesso è che vi siano
3 estrazioni per settimana. Poiché da regolamento
occorre giocare almeno due sestine alla volta, con giocate indefesse di due
sestine è lecito aspettarsi un 3 all'anno...
- La quinta colonna
rappresenta per ciascuna riga il rapporto fra la probabilità di realizzare
il punteggio indicato nella prima colonna della stessa riga, e quella di
realizzare il punteggio della riga precedente. In soldoni, ad esempio l'83
presente nella quinta colonna della riga del 5 indica che è 83 volte
più facile realizzare un 5 che un 5+1.
Verifiche
dei risultati
 Tutti
i calcoli e considerazioni qui sopra sono passibili di dubbi, incertezze e
contestazioni; come essere ragionevolmente sicuri che siano corretti?
Necessariamente, un approccio realmente scientifico richiede verifiche
sperimentali e/o teoriche, quest'ultime condotte con criteri indipendenti e che,
se non danno certezze assolute (quando in accordo...; se in disaccordo le danno
e come...), almeno confortano sul fatto che in qualche caso pratico le cose
funzionino...
Tutti
i calcoli e considerazioni qui sopra sono passibili di dubbi, incertezze e
contestazioni; come essere ragionevolmente sicuri che siano corretti?
Necessariamente, un approccio realmente scientifico richiede verifiche
sperimentali e/o teoriche, quest'ultime condotte con criteri indipendenti e che,
se non danno certezze assolute (quando in accordo...; se in disaccordo le danno
e come...), almeno confortano sul fatto che in qualche caso pratico le cose
funzionino...
Un primo paio di
verifiche parziali è stato esposto sopra nel paragrafo Qualche
verifica intermedia; si è visto che quadrava il numero complessivo di
Possibilità con la somma delle singole, e che due metodi di calcolo
indipendenti per N0
fornivano lo stesso risultato. Ma questo può non esser sufficiente a
rassicurare, per cui ci si può sempre aspettare che spunti fuori una
confutazione...
Per minimizzare le
possibilità di confutazione, si è allora provveduto ad identificare una serie di
metodi di verifica, di seguito esposti, che si spera rasserenino il maggior
numero possibile di dubbiosi.
Metodo 1;
verifica sperimentale spinta
Il regolamento
del gioco del Superenalotto prevede che, nel compilare le schedine, si possano
compendiare giocate
multiple su singoli Pannelli,
ciascuno dei quali contiene i 90 numeri relativi al gioco. Al minimo, per un
Pannello è prevista la selezione di 6 numeri, e ciò comporta la giocata di una
sola sestina; al massimo, si possono selezionare 20 numeri in un Pannello, ciò comportando
invece la giocata contemporanea di 38·760 sestine. Vi sono in giro
schedine con 5 Pannelli, come quella mostrata sotto a destra, che permettono quindi di
giocare 5·38·760=193·800 sestine su ciascuna di esse.
Il procedimento di verifica sperimentale spinta è allora quello che segue:
-
Procurarsi 3·213
di tali schedine, e compilarle in modo da coprire tutte e sole le 622·614·630
sestine che possono venire estratte
-
Recarsi quindi ad uno
sportello Bancomat, ed eseguire un prelievo: inserito il PIN ***** e
ricevuta conferma, quando
il terminale richiede l'importo fra le possibilità 50 €, 100
€, 150 €, 200 €, 250 € o Altro Importo, si
selezioni Altro Importo
Importo
-
Digitare poi una
cifra pari a 311·307·315 €, ed incassare l'Importo
-
Andare in una qualsiasi
ricevitoria e giocare le 3·213 schedine, pagando col denaro
appena prelevato
-
Tornare a casa con
tutte le schedine in tasca (procurandosi preventivamente una giacca con tasche di
dimensione adeguata)
-
Attendere la
successiva estrazione del Superenalotto
-
Verificare sulle 3·213
schedine accumulate a casa che si siano realizzate vincite (e non vincite)
come segue:
Se tutto corrisponde,
i calcoli di cui sopra hanno una discreta probabilità di esser corretti...
Metodo
2;
verifica sperimentale economica
Se, nell'applicare il Metodo
1 sopra descritto, il Bancomat per una qualche oscura ragione rifiuta di
erogare i 311·307·315 €
richiesti, procedere
come segue:
-
Procurarsi 1·729·486
fogli di carta formato A4; con risme di 500 fogli ciascuna, bastano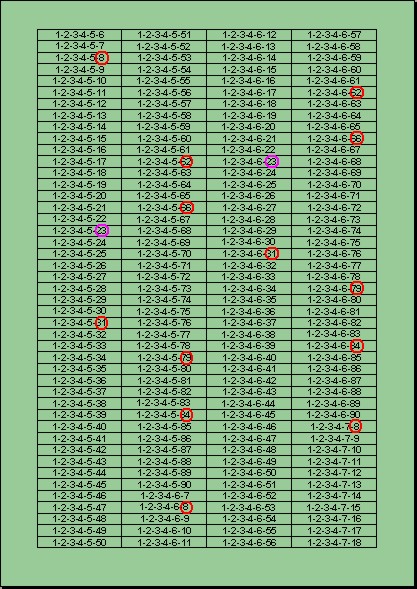 3·459
risme.
A 2,2 € alla risma (costo indicativo al 6 settembre 2009), la spesa è contenuta, poco più
di 7·600
€...
3·459
risme.
A 2,2 € alla risma (costo indicativo al 6 settembre 2009), la spesa è contenuta, poco più
di 7·600
€...
-
Su ciascun foglio è
agevolmente possibile trascrivere 180 sestine per facciata (fronte e retro), come mostrato a
destra per le prime 180; occorre allora utilizzare i fogli per elencare tutte le 622·614·630
possibilità (e avanza qualcosa sulla penultima facciata; e poi l'ultima resta
bianca, quindi utile per qualche appunto...)
-
Attendere la
successiva estrazione del Superenalotto
-
Cerchiare a penna in rosso
tutti i numeri estratti della sestina base, ovunque i fogli A4 li contengano;
ed in fucsia
il numero Jolly, ovunque appaia
-
Se, ad esempio, i
numeri estratti fossero (8,
31,
62,
66,
79,
84),
con Jolly 23,
i numeri andrebbero evidenziati sui fogli A4 come nell'esempio a destra
-
Esaminare
attentamente sui fogli A4 così aggiornati tutte le 622·614·630
possibilità, ripartendole per Categorie come segue, in base al
numero di cerchiature:
-
quelle con
nessuna cerchiatura, oppure con 1 cerchiatura fucsia
senza cerchiature rosse,
nella Categoria 0
-
quelle con 1
cerchiatura rossa,
oppure con 1 cerchiatura rossa
ed 1 fucsia,
nella Categoria 1
-
quelle con 2
cerchiature rosse,
oppure con 2 cerchiature rosse
ed 1 fucsia,
nella Categoria 2
-
quelle con 3
cerchiature rosse,
oppure con 3 cerchiature rosse
ed 1 fucsia,
nella Categoria 3
-
quelle con 4
cerchiature rosse,
oppure con 4 cerchiature rosse
ed 1 fucsia,
nella Categoria 4
-
quelle con 5
cerchiature rosse
e nessuna cerchiatura fucsia,
nella Categoria 5
-
quelle con 5
cerchiature rosse
ed 1 fucsia,
nella Categoria 5+1
-
quelle con 6
cerchiature rosse,
nella Categoria 6
-
Verificare che il
numero di possibilità per ciascuna Categoria risulti come segue:
-
1 in Categoria
6
-
6 in Categoria
5+1
-
498 in Categoria
5
-
52·290
in Categoria 4
-
1·905·680
in Categoria 3
-
28·942·515
in Categoria 2
-
185·232·096
in Categoria 1
-
406·481·544
in Categoria 0
Se tutto corrisponde,
i calcoli di cui sopra hanno una discreta probabilità di esser corretti...
Metodo
3;
verifica computazionale
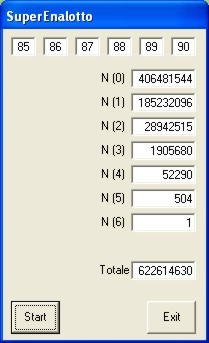 Si
possono a piacimento stilare programmi per calcolatore che, fissata una
qualsiasi sestina giocata, scandiscano tutte le 622·614·630
possibili sestine che possano capitare in una qualsiasi estrazione, verificando
per ciascuna di esse il punteggio conseguito; a sinistra un esempio della
schermata finale di uno di essi (che però non tiene conto del 5+1).
Si
possono a piacimento stilare programmi per calcolatore che, fissata una
qualsiasi sestina giocata, scandiscano tutte le 622·614·630
possibili sestine che possano capitare in una qualsiasi estrazione, verificando
per ciascuna di esse il punteggio conseguito; a sinistra un esempio della
schermata finale di uno di essi (che però non tiene conto del 5+1).
Se tutti i valori
riscontrati per i fattori N corrispondono, come nel caso illustrato,
i calcoli di cui sopra hanno una discreta probabilità di esser corretti...
Per la cronaca, il
programma di cui a sinistra impiega circa 67" per le sue elaborazioni...
Metodo
4;
verifica matematico/pratico/induttiva
Fissate le regole
generali del Superenalotto, le formule sopra riportate, ricavate per i vari
valori dei fattori N, sono in fondo relative ad un caso particolare, cioè
quello con giusto 90 numeri estraibili, ed esattamente 6 numeri da
indovinare. Una verifica pratica di tutte le 622·614·630
possibilità è ciò che si può concettualmente ipotizzar di fare, come
nel Metodo 2 qui sopra, ma nella realtà in nessuna cartoleria troveremo le
3·459 risme di fogli A4, né alcuno disposto a riempirli...
Si può allora cercare di
generalizzare quelle formule, con K arbitrari numeri estraibili e W altrettanto
arbitrari numeri da indovinare (cioè non più una sestina, ma una W-ina), per
poi provare a vedere se le formule funzionano fissando K e W sufficientemente
piccoli, tali da consentire una concreta elencazione di tutti i casi possibili.
Ad esempio se, invece
di 90, i numeri estraibili fossero 6; e se invece di 6 quelli da indovinare
fossero 4, le 622·614·630 possibilità del caso reale
del Superenalotto si ridurrebbero alle seguenti 360:

Le combinazioni non
sono pochissime, ma con un po' di pazienza si può verificare (a mano o
quasi...) se le formule utilizzate per il caso standard funzionano (opportunamente
adattate) anche per questo caso ridotto, o per altri altrettanto
maneggevoli...
Se sì, allora i calcoli di cui sopra
per il caso standard hanno una discreta probabilità di esser corretti...
________________________________
Due dei quattro Metodi
di verifica sopra illustrati sono stati effettivamente utilizzati per
controllare i risultati riassunti nel Riepilogo,
con esito positivo. Si lascia al diligente lettore indovinare quali, e lo si
invita a tentar di riapplicarli, tutti o in parte, ad ulteriore verifica...
Perché non si
dovrebbe mai e poi mai giocare al Superenalotto
In linea di principio
ciascuno Stato, o meglio ciascun Governo di un qualsivoglia Stato, cerca o
dovrebbe principalmente cercare di far quadrare il bilancio. Cioè compensare le
spese complessive con gli introiti, altrettanto complessivi.
Inevitabilmente e
dappertutto, una delle principali
fonti di introito per lo Stato, oltre alle tasse, è il Gioco;
più la popolazione di uno Stato gioca (ovviamente si parla di metodi leciti, cioè approvati
e gestiti dallo Stato), più lo Stato incamera, in quanto esso
incetta una parte prestabilita e definita delle giocate, indipendentemente o
quasi dalle vincite delle fortunate persone che occasionalmente ne usufruiscono.
Il quasi è riferito ad esempio al gioco del Lotto tradizionale: lì in
astratto una sbalorditiva serie di coincidenze ipotetiche potrebbe far vincere migliaia di
cinquine contemporaneamente, mandando in rosso lo Stato; ciò non può avvenire
invece per Totocalcio e Superenalotto, dove le vincite sono invece una percentuale definita
delle giocate, e lo Stato non ci rimette mai, nemmeno nelle più
fantasiose astrazioni concettuali.
Per lo Stato, o se
volete per il Governo, qualsiasi esso sia, il Gioco rappresenta una fonte
inestimabile di introito e vantaggi, per più ragioni:
-
porta considerevoli
quantità di danaro nelle casse dell'Erario (un paio di miliardi di €
all'anno dal solo Superenalotto)
-
questo prelievo
erariale avviene su base volontaria (anche se non sempre consapevole) da
parte di chi gioca; se tutti insorgono e protestano se le aliquote Irpef
vengono elevate di mezzo punto, nessuno protesta nel venir depredato in una percentuale
che è almeno doppia dell'Irpef, quando partecipa ai Giochi di
Stato
-
il Gioco, nel
complesso, crea posti di lavoro; in Italia vi sono 10-20.000 ricevitorie, ed
il loro funzionamento non costa nulla allo Stato, in quanto è pagato da una
percentuale delle giocate. Inoltre, il reddito prodotto dai gestori è
ovviamente soggetto a tassazione, e questo dirotta indirettamente un'altra
parte delle giocate nelle casse dell'Erario
L'ammontare delle
giocate, per il Superenalotto, viene ripartito come mostrato qui a destra; nel 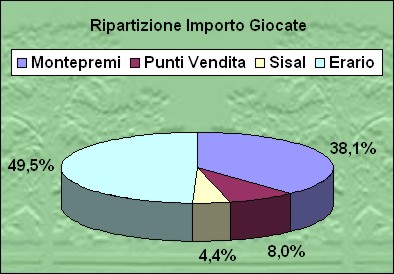 complesso,
le detrazioni tolgono al montepremi il
61,9% dell'importo delle giocate; a paragone, le aliquote Irpef appaiono
come gentili elemosine.
complesso,
le detrazioni tolgono al montepremi il
61,9% dell'importo delle giocate; a paragone, le aliquote Irpef appaiono
come gentili elemosine.
In
fondo, tutto ciò va a vantaggio di chi non gioca: se in astratto
sparisse questa straordinaria fonte di incassi per lo Stato, il Governo (qualsiasi
Governo, per essere Politically Correct) sarebbe 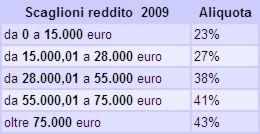 costretto in qualche modo a rimpiazzarla, semmai aumentando l'Irpef o chissà
quale altra tassa, colpendo
quindi anche coloro che non si sottopongono all'autotassazione volontaria
del gioco... Il non giocare, allora, premia doppiamente; in primis, non
si regala allo Stato il 61,9% delle proprie eventuali giocate; e poi si
usufruisce della copertura di tasse o altri oneri pagati invece dagli incauti
giocatori.
costretto in qualche modo a rimpiazzarla, semmai aumentando l'Irpef o chissà
quale altra tassa, colpendo
quindi anche coloro che non si sottopongono all'autotassazione volontaria
del gioco... Il non giocare, allora, premia doppiamente; in primis, non
si regala allo Stato il 61,9% delle proprie eventuali giocate; e poi si
usufruisce della copertura di tasse o altri oneri pagati invece dagli incauti
giocatori.
Per
il Superenalotto, delle
622·614·630 sestine giocabili, appena 1·958·475
sono vincenti, considerando il complesso dei punteggi dal 3 al 6; quindi il 38,1% delle
giocate che appare nel grafico a torta qui sopra viene ridistribuito in qualche
modo allo 0,3% circa dei giocatori. Sembra una ripartizione degna della tirannide più
feroce ed iniqua concepibile: il Supremo Imperatore incamera quasi metà degli
introiti (49,5%),
chiede poi ancora più del 12% per mantenere in vita il meccanismo di esazione, e
destina ciò che resta alla sua Corte, un contribuente su 300, gli eletti che
realizzano 3 punti o più...
Vediamo
adesso cosa capita a questo misero 38,1% che viene restituito ai giocatori sotto forma di
vincite, disinteressandoci volutamente della moltitudine che non vince (cioè il 99,7% degli scommettitori
che realizzano 2, 1 o 0, e che sono lì solo per contribuire alla creazione del
tesoro trisettimanale). Il montepremi viene ripartito fra le categorie
vincenti in base a percentuali fisse, e per ciascuna categoria
l'ammontare viene poi distribuito fra gli appartenenti alla categoria
stessa.
Se
non esistesse il 5+1, un criterio di ripartizione fra le categorie
potrebbe essere l'assegnare il 25% del totale a ciascuna di esse, quelle dei 6,
dei 5, dei 4 e dei 3. In fondo, le categorie derivano in modo naturale
dalla struttura del gioco; questo criterio comunque crea una classe di altissima
eccellenza alla Corte dell'Imperatore (i 6, l'alta Nobiltà), una più larga di
Feudatari (i 5), una ancor più vasta di Funzionari di Palazzo (i 4), ed infine
uno stuolo di Postulanti e Faccendieri (i 3).
I
5+1 rendono ancor più sperequativa la ripartizione; si ricordi che il 5+1 è
una costola del 5, nel senso che (dal punto di vista probabilistico) i
5+1 non sono altro che dei normali 5 che hanno subito una mutazione, un
intervento chirurgico o genetico che li trasforma in simulacri dei 6, insomma dei Feudatari
di primo Rango, ma artefatti... Quindi la fetta di montepremi destinata ai 5+1 dovrebbe venire
esclusivamente prelevata da quella dei 5, assegnando, chessò, il 10% del totale al 5+1 ed il
15% al 5 secco...
Invece
no; la ripartizione del montepremi in categorie avviene come da immagine
a lato: per creare la categoria fittizia dei 5+1 quel che accade è che si sacrifica un po'
quella dei 6, e si interviene pesantemente su quella dei 4. Quella dei 5,
apparentemente altrettanto penalizzata di quella dei 4, in realtà trova una parziale compensazione proprio nella creazione dei 5+1, loro costola... E
i 3? Crescono sorprendentemente al 30%... E' un po' come se il Sovrano, per
rintuzzare le proteste delle categorie penalizzate dalla creazione dei 5+1,
cercasse consenso populista nella moltitudine dei 3...
parziale compensazione proprio nella creazione dei 5+1, loro costola... E
i 3? Crescono sorprendentemente al 30%... E' un po' come se il Sovrano, per
rintuzzare le proteste delle categorie penalizzate dalla creazione dei 5+1,
cercasse consenso populista nella moltitudine dei 3...
In
realtà, la ripartizione effettiva mostrata a lato è accuratamente studiata per creare effetti
emotivi e psicologici che inducano a giocare... La categoria dei 6 serve
a creare il miraggio, ad indurre sogni impossibili, a far balenare visioni...
Come osserva giustamente Marco
Cattaneo nel suo Blog sul sito de Le
Scienze, le cifre che il Jackpot raggiunge sono al di là del
comprensibile per la stragrande maggioranza delle persone; un paio di milioni di
€, o anche meno, già cambiano la vita di (quasi) chiunque, che bisogno c'è
allora di strutturare il gioco in modo che si possa arrivare a 100 milioni e anche
oltre? La ragione è quella esposta sopra: le vincite a 9 cifre servono
esclusivamente a catturare come per le falene fa una lampadina il maggior numero di
scommettitori possibile... Ad irretire l'immaginario con scenari sbalorditivi
oltre ogni limite...
Se
non ci fosse il 6, il 5+1 sarebbe un equilibrato primo premio per un gioco del
tipo del Superenalotto; solitamente produce vincite dell'ordine di 1 milione di
€ o simile, ed è quello che ci si aspetterebbe da una lotteria: cambiare la vita
nella stragrande maggioranza dei casi, ma senza assurdità esagerate come il 6
invece fa.
I 5 ed i 4 sono ragionevoli premi di consolazione per un
siffatto gioco a premi; se uno
gioca in modo indefesso un paio di sestine in tutti i concorsi per una vita intera,
può attendersi concretamente di realizzare qualche 4, i più fortunati un 5. Il
valore dei premi, seppur penalizzato dalla decurtazione dovuta all'introduzione
del 5+1, resta appetibile ma, soprattutto, il fatto che ad ogni estrazione vi
siano decine di vincenti con 5 punti e migliaia con 4 induce i più a pensare
che vincere non sia poi tanto difficile, e che valga la pena di tentare.
Altra
storia per i 3; in un gioco congegnato seriamente, questa categoria di premi non dovrebbe
neppure esistere: paga cifre ridicole in caso di vincita, 15 o 20 € di norma,
cioè una presa in giro assoluta. Ma, ancora una volta, risulta utile per indurre dipendenza
psicologica:  tutti coloro che giocano
con un minimo di assiduità, anche solo 2 o 3 sestine alla volta, ogni tanto un
3 lo realizzano. In un anno vi sono circa 150 estrazioni, e con 2 sestine per
concorso si consegue un 3 mediamente una volta all'anno: questo fornisce ai
giocatori la prova concreta che sì, è possibile vincere, e allora tentiamo ancora ché
la prossima volta andrà meglio... E il fatto che la fetta di montepremi per il
3 sia
gonfiata al 30%, probabilmente serve a garantire che le vincite, seppur minime,
quantomeno compensino il valore delle giocate... Se, nei rari casi di vincita,
si incassasse meno di quanto si è speso per giocare, scatterebbero in molti meccanismi
psicologici di rifiuto... Lo zuccherino elargito di tanto in tanto sarà pure
raro e quasi impalpabile, ma almeno che sia dolce...
tutti coloro che giocano
con un minimo di assiduità, anche solo 2 o 3 sestine alla volta, ogni tanto un
3 lo realizzano. In un anno vi sono circa 150 estrazioni, e con 2 sestine per
concorso si consegue un 3 mediamente una volta all'anno: questo fornisce ai
giocatori la prova concreta che sì, è possibile vincere, e allora tentiamo ancora ché
la prossima volta andrà meglio... E il fatto che la fetta di montepremi per il
3 sia
gonfiata al 30%, probabilmente serve a garantire che le vincite, seppur minime,
quantomeno compensino il valore delle giocate... Se, nei rari casi di vincita,
si incassasse meno di quanto si è speso per giocare, scatterebbero in molti meccanismi
psicologici di rifiuto... Lo zuccherino elargito di tanto in tanto sarà pure
raro e quasi impalpabile, ma almeno che sia dolce...
In
conclusione, ferma restando l'assurdità dell'abnorme prelievo alla fonte che
mutila drasticamente il montepremi, il Superenalotto potrebbe diventare più
ragionevole se:
-
si riducesse
drasticamente la percentuale destinata alla categoria 6; portarla dal
20% al 5%, ad esempio, manterrebbe le relative vincite ancora nell'ambito delle decine
di milioni di €, tali cioè da conservare l'effetto sogno ad occhi aperti,
e restituirebbe un discreto valore in più alle categorie inferiori...
-
si abolisse la categoria
dei 3; in fondo, il Totocalcio funzionava anche solo col 13 e col 12...
Scendere fino al 3 al Superenalotto è ridicolo, somiglia ai premi da
lotteria dell'oratorio, tre saponette o un portacenere...
-
si irrobustissero le categorie
dei 4 e dei 5; prendendo profitto dalla riduzione del 6 e dall'abolizione
del 3, queste dovrebbero costituire il nucleo forte delle aspettative del Gioco...
Perché io gioco
sempre al Superenalotto
 Essendo
il predicare bene ed il razzolare male una moda conclamata,
ebbene sì, ammetto di
razzolare male, alla
moda appunto. Nel senso che gioco al Superenalotto ad ogni concorso,
nonostante quanto sopra esposto...
Essendo
il predicare bene ed il razzolare male una moda conclamata,
ebbene sì, ammetto di
razzolare male, alla
moda appunto. Nel senso che gioco al Superenalotto ad ogni concorso,
nonostante quanto sopra esposto...
Vi sono tre o quattro
motivi, criticabili quanto si voglia, per cui può valere la pena di giocare una
qualche sestina al Superenalotto; proverò adesso a discuterne...
-
Il gioco del
Superenalotto esiste, è un dato di fatto, e non possiamo ignorarlo, nonostante la sua assurdità
intrinseca. Accade inevitabilmente che talvolta
qualcuno vinca cifre inconcepibili; la reazione comune verso i benedetti
dalla sorte è di disgusto, di somma invidia, di repulsione, di maledizione,
di bestemmia, di sconcerto. Ma per poterli davvero condannare per reato
di somma fortuna, questi vincitori, occorre essere parte del gioco.
Nel senso che non si ha il diritto di dire che cu... se
non si è partecipato... Chi stramaledice i vincitori senza aver giocato a
sua volta è un po' come chi dice governo ladro ma non va mai a
votare... E quindi una quota parte delle modeste giocate trisettimanali
serve a comprarsi il diritto di improperio...
-
Un'altra quota parte
delle giocate rientra poi effettivamente nelle tasche: come visto sopra,
l'assiduità fa recuperare una media del 38,1% di quanto speso... I
risultati empirici personali confermano grossomodo la faccenda, con quattro
o cinque 3 realizzati negli anni...
-
Supponiamo che il
concorso del 26 settembre 2009 qui a destra costituisca un caso tipico:
quasi 6 milioni di € di montepremi corrispondono a più di 15 milioni di €
giocati, pari più o meno a 30 milioni di sestine, cioè una ogni due italiani. Non è
consentito giocare meno di 2 sestine, per cui se tutti coloro che partecipano
giocassero 2 sestine, gli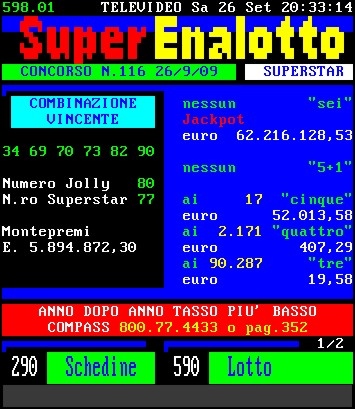 scommettitori sarebbero 15 milioni. Immagino che sia così per molti dei
partecipanti, ma vi sono anche quelli che giocano più sestine o addirittura
costosissimi sistemi... Se la media complessiva la stimiamo in 5 o 6 sestine
pro capite, i giocatori sono quindi fra i 5 ed i 6 milioni. Chiaramente,
più sestine si giocano, più cresce la probabilità di vincere qualcosa;
con 2 sestine lo 0,6%, con 4 l'1,2%, e così via. Passare da 2 a 4 sestine
fa raddoppiare le probabilità di vincita, ma passare da 4 a 6 le fa
crescere solo del 50%, e comunque rimangono bassissime... Ancor peggio
l'incremento percentuale man mano che si accresce il numero di sestine
giocate... Possiamo allora immaginare di suddividere gli italiani in
categorie come segue (ovviamente le quantità sono solo indicative; conta
qui l'aspetto qualitativo...):
scommettitori sarebbero 15 milioni. Immagino che sia così per molti dei
partecipanti, ma vi sono anche quelli che giocano più sestine o addirittura
costosissimi sistemi... Se la media complessiva la stimiamo in 5 o 6 sestine
pro capite, i giocatori sono quindi fra i 5 ed i 6 milioni. Chiaramente,
più sestine si giocano, più cresce la probabilità di vincere qualcosa;
con 2 sestine lo 0,6%, con 4 l'1,2%, e così via. Passare da 2 a 4 sestine
fa raddoppiare le probabilità di vincita, ma passare da 4 a 6 le fa
crescere solo del 50%, e comunque rimangono bassissime... Ancor peggio
l'incremento percentuale man mano che si accresce il numero di sestine
giocate... Possiamo allora immaginare di suddividere gli italiani in
categorie come segue (ovviamente le quantità sono solo indicative; conta
qui l'aspetto qualitativo...):
-
54 milioni di
italiani non giocano affatto, ed hanno lo 0,0% di probabilità di
vincere qualcosa
-
3 milioni di
italiani giocano 2 sestine alla volta, ed hanno lo 0,6% di probabilità
di vincere qualcosa
-
2 milioni di
italiani giocano 3 o 4 sestine alla volta, ed hanno fra lo 0,9% e l'1,2%
di probabilità di vincere qualcosa
-
1 milione di
italiani gioca da 5 a
622·614·630 sestine alla volta, ed ha fra l'1,5% ed il
100% di probabilità di vincere qualcosa
Decidere di passare
dalla 2a alla 3a categoria fa come visto sopra
raddoppiare le probabilità... Ma il decidere di passare dalla 1a
alla 2a comporta un incremento di tali probabilità pari a:
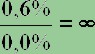
L'incremento delle
speranze è sbalorditivo, al modesto prezzo di 1€ alla volta...
-
Se si va al Luna Park
e si decide di fare un giro sulle montagne russe, al ritorno a casa ci si
ritrova con qualche € in meno in tasca e niente di concreto nelle mani; si
è scelto di spendere qualcosa per pagarsi una Emozione. Ciò a dire
che non è vero che quando spendiamo i nostri soldi ci aspettiamo sempre un
ritorno concreto e tangibile: fra le cose per le quali si è disposti a
cacciar soldi vi sono anche quelle impalpabili e prive di
consistenza. Come il piccolissimo momento di sospensione del respiro in cui
si va a controllare l'estrazione del Superenalotto... La nostra Ragione è ben
cosciente che le speranze sono infinitesime, ma Emozione è il
contrario di Ragione, e sarà pur lecito mandare i neuroni in vacanza
per un minuto ogni due o tre giorni, smarrendosi fra sogni impossibili... Nessuno sale sulle montagne russe pensando che (siccome
F = m · a
e siccome ovviamente le montagne russe sono progettate al meglio) non capiterà nulla di pericoloso, per cui continua tranquillo a leggere
il giornale anche a testa in giù...
Per concludere, è
ovvio che il giocare (il minimo, naturalmente) non è un investimento o una
concreta speranza di arricchirsi; è solo una spesa consapevole con cui si può scegliere di
pagarsi le piccole cose di cui sopra...
NOTA FINALE
Un paio di giorni fa
(settembre 2009) una notizia alla radio ha segnalato che la prossima Lotteria Italia del 6
gennaio 2010 sarà dotata di due Primi Premi da 5 milioni di € ciascuno,
e non uno soltanto come al solito... Ciò poiché nessuno si è presentato ad incassare il
Primo Premio
del gennaio 2009, che viene quindi rimesso in gioco...
Non si è tenuto conto,
nelle considerazioni di cui sopra sul Superenalotto, del fatto che una parte dei premi delle
Lotterie non viene
mai incassata; diversamente dal caso estremo della Lotteria Italia sopra esposto, le vincite
non distribuite non ritornano in circolo, e vanno a far calare ulteriormente le
già misere percentuali destinate agli sporadici vincitori. Perché capita? Beh,
uno dei motivi è che ad esempio in Italia ogni anno avvengono circa 600.000 decessi,
grosso modo l'1% della popolazione. In media, anche l'1% dei giocatori di Superenalotto o
altri giochi a premi defunge, e così vale in proporzione per i vincitori dei suddetti
giochi... Semmai i biglietti vincenti vengono ritrovati ormai scaduti dopo anni in qualche
cassetto, dagli eredi...
29
settembre
2009, Bruno Davide

Vai alla genealogia Torna
a home page Invia informazioni Legge
sulla privacy Copyrights
©
 Fra
il 3 febbraio 2009 (concorso N° 15) ed il 20 agosto del 2009 (concorso N°100),
nessuno riuscì a centrare il mitico 6 al Superenalotto, facendo
quindi levitare il montepremi del Jackpot fino alla stratosferica cifra di 147.807.299,08
€, poi vinti il 22 agosto con un biglietto giocato alla ricevitoria di un bar di Bagnone (Massa
Carrara).
Fra
il 3 febbraio 2009 (concorso N° 15) ed il 20 agosto del 2009 (concorso N°100),
nessuno riuscì a centrare il mitico 6 al Superenalotto, facendo
quindi levitare il montepremi del Jackpot fino alla stratosferica cifra di 147.807.299,08
€, poi vinti il 22 agosto con un biglietto giocato alla ricevitoria di un bar di Bagnone (Massa
Carrara).
 comunque
NON
comunque
NON 
 (45,
31, 78, 2, 29, 16) e (29, 16, 31, 78, 45, 2)
(45,
31, 78, 2, 29, 16) e (29, 16, 31, 78, 45, 2) Un certo numero di esse
permette di far 6, un altra
quantità 5, e così via. In sostanza, per ciascuna sestina da noi giocata,
l'esito può essere uno ed uno solo fra i seguenti 7 casi:
Un certo numero di esse
permette di far 6, un altra
quantità 5, e così via. In sostanza, per ciascuna sestina da noi giocata,
l'esito può essere uno ed uno solo fra i seguenti 7 casi:

 esempio
in precedenza; i due numeri da alterare possiamo sceglierli in 15 modi diversi,
indicati in rosso
nella tabella che segue:
esempio
in precedenza; i due numeri da alterare possiamo sceglierli in 15 modi diversi,
indicati in rosso
nella tabella che segue:




 Tutti
i calcoli e considerazioni qui sopra sono passibili di dubbi, incertezze e
contestazioni; come essere ragionevolmente sicuri che siano corretti?
Necessariamente, un approccio realmente scientifico richiede verifiche
sperimentali e/o teoriche, quest'ultime condotte con criteri indipendenti e che,
se non danno certezze assolute (quando in accordo...; se in disaccordo le danno
e come...), almeno confortano sul fatto che in qualche caso pratico le cose
funzionino...
Tutti
i calcoli e considerazioni qui sopra sono passibili di dubbi, incertezze e
contestazioni; come essere ragionevolmente sicuri che siano corretti?
Necessariamente, un approccio realmente scientifico richiede verifiche
sperimentali e/o teoriche, quest'ultime condotte con criteri indipendenti e che,
se non danno certezze assolute (quando in accordo...; se in disaccordo le danno
e come...), almeno confortano sul fatto che in qualche caso pratico le cose
funzionino... Importo
Importo
 3·459
risme.
A 2,2 € alla risma (costo indicativo al 6 settembre 2009), la spesa è contenuta, poco più
di 7·600
€...
3·459
risme.
A 2,2 € alla risma (costo indicativo al 6 settembre 2009), la spesa è contenuta, poco più
di 7·600
€... Si
possono a piacimento stilare programmi per calcolatore che, fissata una
qualsiasi sestina giocata, scandiscano tutte le 622·614·630
possibili sestine che possano capitare in una qualsiasi estrazione, verificando
per ciascuna di esse il punteggio conseguito; a sinistra un esempio della
schermata finale di uno di essi (che però non tiene conto del 5+1).
Si
possono a piacimento stilare programmi per calcolatore che, fissata una
qualsiasi sestina giocata, scandiscano tutte le 622·614·630
possibili sestine che possano capitare in una qualsiasi estrazione, verificando
per ciascuna di esse il punteggio conseguito; a sinistra un esempio della
schermata finale di uno di essi (che però non tiene conto del 5+1).
 complesso,
le detrazioni tolgono al montepremi il
61,9% dell'importo delle giocate; a paragone, le aliquote Irpef appaiono
come gentili elemosine.
complesso,
le detrazioni tolgono al montepremi il
61,9% dell'importo delle giocate; a paragone, le aliquote Irpef appaiono
come gentili elemosine.
 costretto in qualche modo a rimpiazzarla, semmai aumentando l'Irpef o chissà
quale altra tassa, colpendo
quindi anche coloro che non si sottopongono all'autotassazione volontaria
del gioco... Il non giocare, allora, premia doppiamente; in primis, non
si regala allo Stato il 61,9% delle proprie eventuali giocate; e poi si
usufruisce della copertura di tasse o altri oneri pagati invece dagli incauti
giocatori.
costretto in qualche modo a rimpiazzarla, semmai aumentando l'Irpef o chissà
quale altra tassa, colpendo
quindi anche coloro che non si sottopongono all'autotassazione volontaria
del gioco... Il non giocare, allora, premia doppiamente; in primis, non
si regala allo Stato il 61,9% delle proprie eventuali giocate; e poi si
usufruisce della copertura di tasse o altri oneri pagati invece dagli incauti
giocatori.
 parziale compensazione proprio nella creazione dei 5+1, loro costola... E
i 3? Crescono sorprendentemente al 30%... E' un po' come se il Sovrano, per
rintuzzare le proteste delle categorie penalizzate dalla creazione dei 5+1,
cercasse consenso populista nella moltitudine dei 3...
parziale compensazione proprio nella creazione dei 5+1, loro costola... E
i 3? Crescono sorprendentemente al 30%... E' un po' come se il Sovrano, per
rintuzzare le proteste delle categorie penalizzate dalla creazione dei 5+1,
cercasse consenso populista nella moltitudine dei 3... tutti coloro che giocano
con un minimo di assiduità, anche solo 2 o 3 sestine alla volta, ogni tanto un
3 lo realizzano. In un anno vi sono circa 150 estrazioni, e con 2 sestine per
concorso si consegue un 3 mediamente una volta all'anno: questo fornisce ai
giocatori la prova concreta che sì, è possibile vincere, e allora tentiamo ancora ché
la prossima volta andrà meglio... E il fatto che la fetta di montepremi per il
3 sia
gonfiata al 30%, probabilmente serve a garantire che le vincite, seppur minime,
quantomeno compensino il valore delle giocate... Se, nei rari casi di vincita,
si incassasse meno di quanto si è speso per giocare, scatterebbero in molti meccanismi
psicologici di rifiuto... Lo zuccherino elargito di tanto in tanto sarà pure
raro e quasi impalpabile, ma almeno che sia dolce...
tutti coloro che giocano
con un minimo di assiduità, anche solo 2 o 3 sestine alla volta, ogni tanto un
3 lo realizzano. In un anno vi sono circa 150 estrazioni, e con 2 sestine per
concorso si consegue un 3 mediamente una volta all'anno: questo fornisce ai
giocatori la prova concreta che sì, è possibile vincere, e allora tentiamo ancora ché
la prossima volta andrà meglio... E il fatto che la fetta di montepremi per il
3 sia
gonfiata al 30%, probabilmente serve a garantire che le vincite, seppur minime,
quantomeno compensino il valore delle giocate... Se, nei rari casi di vincita,
si incassasse meno di quanto si è speso per giocare, scatterebbero in molti meccanismi
psicologici di rifiuto... Lo zuccherino elargito di tanto in tanto sarà pure
raro e quasi impalpabile, ma almeno che sia dolce...
 Essendo
il predicare bene ed il razzolare male una moda conclamata,
ebbene sì, ammetto di
razzolare male, alla
moda appunto. Nel senso che gioco al Superenalotto ad ogni concorso,
nonostante quanto sopra esposto...
Essendo
il predicare bene ed il razzolare male una moda conclamata,
ebbene sì, ammetto di
razzolare male, alla
moda appunto. Nel senso che gioco al Superenalotto ad ogni concorso,
nonostante quanto sopra esposto... scommettitori sarebbero 15 milioni. Immagino che sia così per molti dei
partecipanti, ma vi sono anche quelli che giocano più sestine o addirittura
costosissimi sistemi... Se la media complessiva la stimiamo in 5 o 6 sestine
pro capite, i giocatori sono quindi fra i 5 ed i 6 milioni. Chiaramente,
più sestine si giocano, più cresce la probabilità di vincere qualcosa;
con 2 sestine lo 0,6%, con 4 l'1,2%, e così via. Passare da 2 a 4 sestine
fa raddoppiare le probabilità di vincita, ma passare da 4 a 6 le fa
crescere solo del 50%, e comunque rimangono bassissime... Ancor peggio
l'incremento percentuale man mano che si accresce il numero di sestine
giocate... Possiamo allora immaginare di suddividere gli italiani in
categorie come segue (ovviamente le quantità sono solo indicative; conta
qui l'aspetto qualitativo...):
scommettitori sarebbero 15 milioni. Immagino che sia così per molti dei
partecipanti, ma vi sono anche quelli che giocano più sestine o addirittura
costosissimi sistemi... Se la media complessiva la stimiamo in 5 o 6 sestine
pro capite, i giocatori sono quindi fra i 5 ed i 6 milioni. Chiaramente,
più sestine si giocano, più cresce la probabilità di vincere qualcosa;
con 2 sestine lo 0,6%, con 4 l'1,2%, e così via. Passare da 2 a 4 sestine
fa raddoppiare le probabilità di vincita, ma passare da 4 a 6 le fa
crescere solo del 50%, e comunque rimangono bassissime... Ancor peggio
l'incremento percentuale man mano che si accresce il numero di sestine
giocate... Possiamo allora immaginare di suddividere gli italiani in
categorie come segue (ovviamente le quantità sono solo indicative; conta
qui l'aspetto qualitativo...):